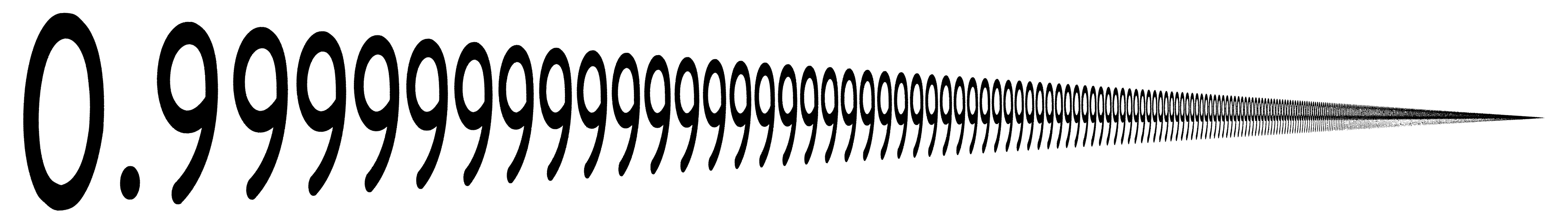
In mathematics, the repeating decimal 0.999... which may also be written as 0.9̇ or 0.(9), denotes a real number that can be shown to be the number one. In other words, the symbols 0.999... and 1 represent the same number.
| 1/3 | = | 0.3333333... | /*3 |
| 3/3 | = | 0.9999999... | |
| 1 | = | 0.9999999... |
Confusing :S? Or not ? ;)
0.999... = lim n->infinity of (sum from i=1 to n of (9*10^(-i))) = 1
ReplyDeletefloor(0.999...) = floor(lim n->infinity of (sum from i=1 to n of (9*10^(-i)))) = floor(1) = 1
[ floor(x) = max{integer z where z <= x} ]
^^